26Mar
池田校マネージャーの長谷川です。
久しぶりに「学力向上の方程式」の話題です。
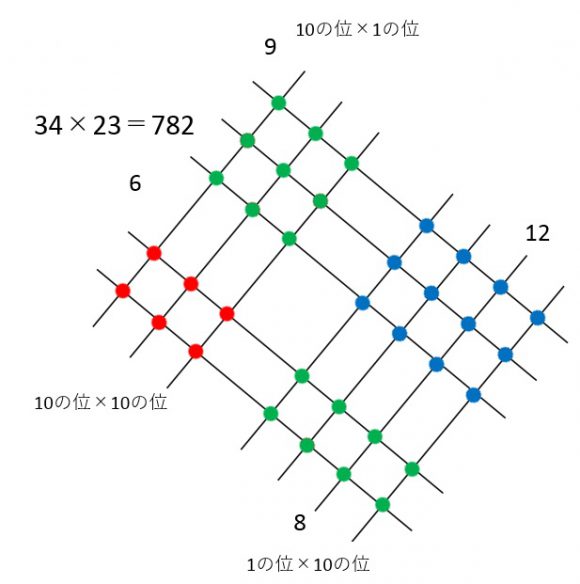
図は、インターネット上で、
ちょっと自慢げに流れてくる画像をマネしたものです。
2ケタ×2ケタの掛け算です。
数をケタごとに線で表し、交点の数が各位の掛け算の答え、
あとはそれを足す、という方法です。
これに似た工夫として、斜めに罫線を引いて、
計算をしてそれぞれのマスに入れる、という方法もあるようです。
なんて事はない?
そんな手間かけるほどのことはない?
その通りです。
でも、これを見ていて思ったのです。
34×23の計算の例でいうと、こんな筆算をする人が多いでしょう。
34
× 23
__102
_+68
_ 782
繰り上がりが少ないので、あまりミスする人はいないと思います。
では、「48×67」ならどうでしょう。8×7=56、
5を小さく書くか、左手を広げて「5」をつくって、
4×7=28に小さく書いた5を足して…ミスしそうですね。
では、こう書いてみたらどうでしょう。
48
__×67
___56
__28
__48
+24
3216
「48×7」、「48×60」を、
一行で書こうとするから間違えるのではないか。
分けて書いたほうが脳に対するストレスも
ミスする可能性も少なくなります。
難問というほどではないですが、大デカルトの教え
「難問は分割せよ」が、ここにも活かせるのではないか。
春の日の日曜日、そんなことを思ったのでした。
なお、中学3年生が春に習う(a+b)2なんて計算でも同じことです。
乗法公式なんて堅苦しく考えなくても
(まあ、これは後に因数分解がくるので仕方が無い面もありますが)
縦に並べて筆算すればええやん、
と自分自身が中学1年生の頃から40年近く思い続けています。












